LIMITLESS LEADS TO LIMIT - The birth of calculus

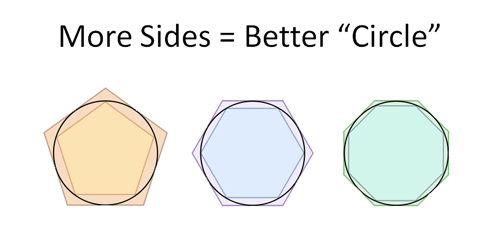
If you go on increase the number of  sides of a polygon. the circle will be the limit.

     1/2^1 + 1/2^2 + 1/2^3 + 1/2^4+........  =1
                           or
     Sum of all the terms of 1/2^n  = 1

     When n goes from 1 to infinity, the sum of the above series approaches 'one'; but never touches 'one' or crosses 'one', however bigger the 'n' may be.  Hence we can say, the limit of the sum of the series is 1.

(1+1/1)^1+ (1+1/2)^2 +(1+1/3)^3 + .....     =2.71... = e
The limit of the above series is the famous Euler constant e.

    The concept of limit is the corner stone of calculus.  Let us see an example.
Let y= x^2
Let dx be the smallest change in x , let dy be the corresponding small change in y.
I want to find dy/dx
Let x be 3, let the small change be 0.1 (dx) The new x is 3.1
corresponding change in y is

                           y=x^2
      old x: 3        9
     new x: 3.1    9.61

hence   dy = 9.61 - 9 = .61
dy/dx = 0.61/0.1 = 6.1
Now  let us give still more small change in x, that is 0.01
                           y=x^2
      old x: 3         9
     new x: 3.01    9.0601
  
Now dy = 9.0601 - 9 = 0.0601
again, dy/dx = 0.0601/0.01 = 6.01

   If we go on give more and more smaller change in 'x' (like .01,.0033,.0001), the dy/dx will approach 6(the limit).  Since x = 3; 6 = 2x.  Hence dy/dx =2x
That is small change in y divided by small change in x yields 2x whatever may be the value of x.
     This is the operation 'division' for continuous functions like growth of a plant, fall of temperature, increase of electric current.  We call this operation as "differentiation".  That is calculus.
     The ordinary 'division' is applicable to only countable things like books, pens, chocolates etc.

Note: 1. if y=sinx
              dy/dx = cosx
           2. If y = x^3
              dy/dx = 3x^2   
           3. If y= 5x
              dy/dx =5    and on and on
The above are proved results from calculus.