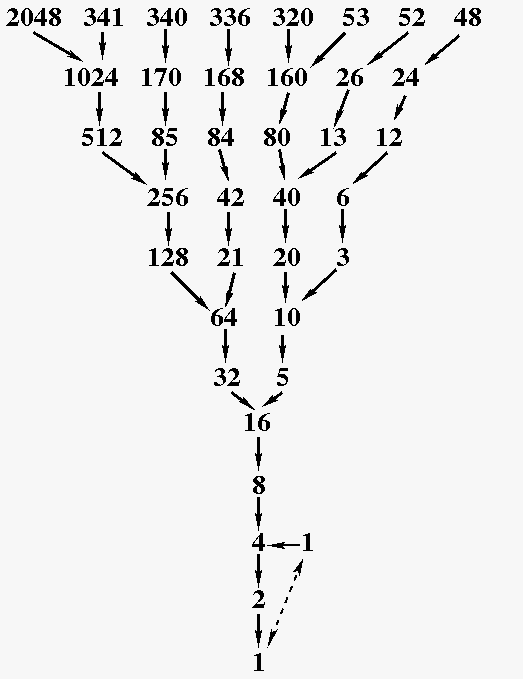A PROBLEM THAT BAFFLES MATHEMATICIANS

We will produce a sequence of numbers following some rules.
1. Take any positive natural integer.
2. If it is even, next term will be half of it.
3. If it is odd, multiply it by three and add one to get next term.
4. Apply the rule no.2 or 3 to the next term and go on produce the sequence.

Let us take an example; consider the number 12. It is even; hence next term is 6, again even; next term is 3. Now it is odd; next term is 3+3+1 = 10. Just proceed like this, we get,
12, 6,3,10,5,16,8,4,2,1

Now let us take 19;
19,58,29,88,44,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1

It seems, we always end up with 8,4,2,1. In fact, all the numbers tested so far (even using the computer) always end up with 8,4,2,1... In other words, this sequence ultimately reaches one.
We know, it is impossible to test the infinite numbers. Is there any mathematical proof that the sequence will always reach one? No, not so far. This problem is called "Collatz conjecture" (assumption). This problem can be easily understood by a 10-year-old. But the mathematics world has not solved the problem even today.
One great mathematician once said, "mathematics is not ready for such problems."
One can easily a write small computer program to produce this sequence. This problem has not practically served any purpose so far. But it can attract youngsters towards mathematics and number theory. Some people say, the solution to the problem carries some prize money. But, remember there is no easy solution to this problem. Anyway, attempt it.
Philosophically, we may arrive at one conclusion. That is, " Even if you multiply something three times, and spend half of it, you will end up with one unit". Is the nature trying to tell us something through Colletz conjecture?

Note;

The stopping time or number of steps to arrive at one does not follow any pattern. It baffles us more. A small computer program to produce the sequence is given here.

---------------------------------------------------------------------------------

Comments

THE EARTH, A SUPER ORGANISM

JOIN MY COURSE: "Become a programmer in a day with python" A man called 'love lock' (what a name) proposed a theory called Gaia theory, named after Greek Goddess. It says, "Earth is a self-regulating organism like a human being. The organic life in it interacts with in-organic matter and maintains atmosphere, temperature and environment". Hence the earth is still suitable for the life to thrive. Imagine, in a particular place, there are lot of flowers. Some flowers are white and some are darkly coloured. We know, white reflects light and heat while dark absorbs the same. White flowers can thrive in hot climate. But dark flowers requires cold climate. The absorption and reflection balances and the environment reaches average, warm temperature at which both the flowers can co-exist. This is the essence of "Gaia" theory. On our earth, ...

DISORDER IS THE "ORDER OF THE DAY"

Imagine a balloon full of air. The air molecules are moving randomly inside the balloon. Let us pierce the balloon with a pin. The air rushes out. Why should not the air molecules stay inside the balloon safely and ignore the little hole? That is not the way the world works. The molecules always "want to occupy as many states as possible". Hence the air goes out in the open to occupy more volume. The things always goes into disorder (entropy) and the disorder increases with time. The above statement is what we call "second law of thermodynamics". Consider a cup of coffee on the table. Suppose the heat from entire room flows to your cup of coffee, the coffee will boil and the rest of the room will freeze. Freezing means bringing things to order and arrangement. It violates the second law. Hence it will never happen. Hence heat must flow from high ...

CASINO'S GAME

Let us find out how the casino survives with mathematics. Say, your friend invite you for a game of dice. You must bet (wager) 2 dollars. If you roll 'six' you will get back 8 dollars. The game will go on for 30 rounds. All sounds good. The probability of rolling 'six' is 1/6. Since the game will be played for 30 times, the 'expected win' is 30*1/6 = 5. That is, you are expected to win 5 rounds out of 30. Hence your gain will be 5 * 8 =40 dollars. ok. This also implies that you will loose 25 rounds. Hence your loss will be 25*2 =50 dollars. Your net gain will be gain-less = 40-50 = -10 dollars. For 30 rounds, the loss is -10 dollars, Hence, for one round =-10/30 = -1/3 dollars. There will be a loss of -1/3 or 0.33 dollars per round. It is not a fair game. Let us make a simple formula to calculate 'Pa...

sciencecapsules

Search This Blog