TRIGNOMETRY IN A NUT-SHELL

Draw a right angled triangle of angle 30 degree as shown in the figure. Let the length of the hypotenuse be 1 unit.
We know sine 30 = opposite/hypotenuse = opposite side/1 unit
Hence sin30 is the length of the opposite side which is 0.5 unit. Hence sin30=0.5
similarly
cosine30=cos30=adjacent /hypotenuse =.87 unit
This ratios sin30 and cos30 holds good for any smaller or larger triangles. We can find any side of the triangle using these ratios.

We can find the sine and cos values for angles from 0 to 90 degree in this way. Also they are available in ready table form. This 'sin and cos' concept is also extended to the angles 91 to 360 degree, Here, we have to incorporate positive and negative signs suitably (refer).

Now,
tan x = sin x/cos x = opp/hyp/ adj/hyp = opp/adj
When 'sin' is divided by 'cos' , the ratio of opposite side/ adjacent side is obtained. We call it 'tan'. (tangent)

Say, you are standing 40 m from a tall building and you are viewing the top of the building. Say, the viewing angle is 45 degree from the horizontal.
Here the line of sight is the 'hypotenuse', building is the 'opposite side' and the distance between yourself and the building is adjacent. The tan45 is 1. That means, adjacent and opposite must be equal. The building height must be 40 m. This is just one example for the use of trigonometry.

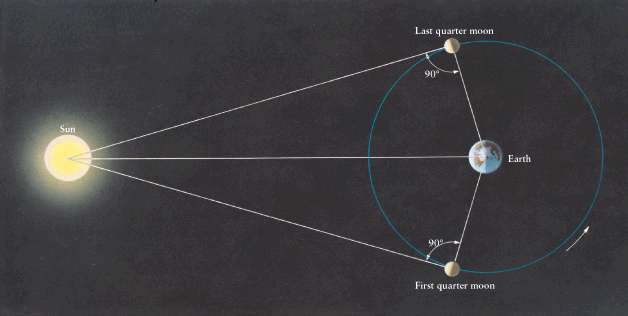
Sun, Earth and moon sometimes form a right angled triangle. Atoms may lie in a triangle. Trigonometry can be applied in both the cases. That is real beauty.

From sin and cos, hundreds of trignometric functions and formulas can be derived.
for example;
sin^2x + cos^2 x = 1
in our case (.5)^2 + (.87)^2
for 30 degree .25 +.75 =1 verified.
The above equation is the trigonometric form of Pythagoras theorem.

Light ray practically travels in straight line. Hence, in geometrical optics, trigonometry is widely used.
The value of sine function for 0 to 360 degree oscillates between 0 -1- 0- (-1). Hence a wave form is created. Sine wave is applied everywhere in physics.
The trigonometry connects, distance, angle, circle, waves using compact functions like sin x.

Comments

THE EARTH, A SUPER ORGANISM

JOIN MY COURSE: "Become a programmer in a day with python" A man called 'love lock' (what a name) proposed a theory called Gaia theory, named after Greek Goddess. It says, "Earth is a self-regulating organism like a human being. The organic life in it interacts with in-organic matter and maintains atmosphere, temperature and environment". Hence the earth is still suitable for the life to thrive. Imagine, in a particular place, there are lot of flowers. Some flowers are white and some are darkly coloured. We know, white reflects light and heat while dark absorbs the same. White flowers can thrive in hot climate. But dark flowers requires cold climate. The absorption and reflection balances and the environment reaches average, warm temperature at which both the flowers can co-exist. This is the essence of "Gaia" theory. On our earth, ...

THE PARABOLA

A jet of water shooting from a hose pipe will follow a parabolic path. What is the so special about parabola. Y= x^2 Draw a graph for the above equation. It will result in a parabola. This parabola is also called unit parabola. Any equation involving square will yield a parabola. Example: Y = 2x^2 +3x+3 (also called quadratic equation) X= 2 and -2, both satisfies the equation 4 = X^2. Parabolic equations always have two solutions. Any motion taking place freely under gravity follows parabolic path. Examples: An object dropped from a moving train, A bomb dropped from flying plane, A ball kicked upwards. If a beam of light rays fall on the parabolic shaped mirror, they will be reflected and brought to focus on a point. This fact is made use of in Dish Antenna, Telescope mirrors, etc. ...

DISORDER IS THE "ORDER OF THE DAY"

Imagine a balloon full of air. The air molecules are moving randomly inside the balloon. Let us pierce the balloon with a pin. The air rushes out. Why should not the air molecules stay inside the balloon safely and ignore the little hole? That is not the way the world works. The molecules always "want to occupy as many states as possible". Hence the air goes out in the open to occupy more volume. The things always goes into disorder (entropy) and the disorder increases with time. The above statement is what we call "second law of thermodynamics". Consider a cup of coffee on the table. Suppose the heat from entire room flows to your cup of coffee, the coffee will boil and the rest of the room will freeze. Freezing means bringing things to order and arrangement. It violates the second law. Hence it will never happen. Hence heat must flow from high ...

sciencecapsules

Search This Blog