EYE CANDY

 

  Take the point C[ -2+i] in the complex plane.  Let Z =0 +0i and square it. Z^2 = 0+0i..  Now add C = Z  to Z^2 and get Z1.

Z1 = Z^2+C
Z1 = [0+0i]^2+[-2+i]
Z1 = -2+i

now let Z=Z1 and calculate
Z1 = Z^2+C  again
    = [-2+i]^2+[-2+i]
    = 1+5i
[complex addition,multiplication used]

Magnitude of Z1 [1+5i] = root of [1^2+5^2] = 5.09  

  Now do this repetitive feed back calculation say 100  times according to this formula. 

Z[n+1] = Z[n]^2+C

Each time calculate the magnitude of Z.  If the magnitude stay stable within 2, paint the point C as black.  If the magnitude goes beyond 2 and heads towards infinity, either paint the point as white or the point may be given colours as follows.  If the magnitude goes beyond 2 after 10  iterations, the point C may be given red.  For 20 iterations, it may be a orange dot.  For 30  repetitions, C may be given yellow.  So the colours are chosen according to the programmers taste.

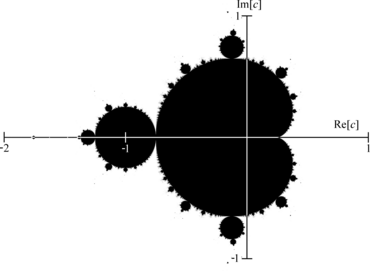
    For all the points C in the complex plane[starting Z as 0+0i], do this repetitive calculations and colouring.  We get a nice picture as given above.  The points in the black area is called mandalbrot set.  This is the curious mathematical art.

                                                  

     This art has symmetry, self similarity and details.  The pattern in  the macroscopic level is also repeated at microscopic level like a tree.  When we do more repetitions, we get more details.  We can zoom in and explore the picture inch by inch like exploring a country.  From a simple equation we get a complex beautiful art.  It belongs to fractal's family.

     Mandalbrot set is used today in cryptography.  People now compare this fractal to universe and try to represent universe by numbers.

This art is best described by Keat's poem.
"Charmed magic casements, opening on the foam
Of perilous seas, in fairy lands forlorn".